O triângulo equilátero, um símbolo perfeito para o RER
Por que o triângulo equilateral foi escolhido para simbolizar a Divindade?
Veremos que as propriedades do triângulo equilátero são notáveis pela perfeição simétrica. Os direitos particulares, bissecção, mediadores, medianas são confusos, de modo que há apenas três retas notáveis que são ao mesmo tempo eixos de simetria da figura e cuja intersecção se torna o centro de uma rotação axial.
 A Deidade perfeita da qual somos a imagem imortal, é, portanto, representada em sua dimensão trinitária cristã pelo triângulo equilátero. Falamos de uma trindade, mas na geometria é um ternário perfeito. Neste ponto, devemos entender que o símbolo está estruturando para a mente e o espírito humano. Deve-se notar que as três retas notáveis do triângulo dos topos são simplesmente perpendiculares, instrumentos e joias conhecidas dos maçons retificados. Você também pode obter essas retas notáveis de um fio de prumo, colocando-o no topo. A base do triângulo também é perfeitamente horizontal.
A Deidade perfeita da qual somos a imagem imortal, é, portanto, representada em sua dimensão trinitária cristã pelo triângulo equilátero. Falamos de uma trindade, mas na geometria é um ternário perfeito. Neste ponto, devemos entender que o símbolo está estruturando para a mente e o espírito humano. Deve-se notar que as três retas notáveis do triângulo dos topos são simplesmente perpendiculares, instrumentos e joias conhecidas dos maçons retificados. Você também pode obter essas retas notáveis de um fio de prumo, colocando-o no topo. A base do triângulo também é perfeitamente horizontal.
Na geometria euclidiana, um triângulo equilátero é um triângulo cujos três lados têm o mesmo comprimento. Seus três ângulos internos são a mesma medição de 60 graus, tornando-o um polígono normal de três picos. Todos os triângulos equilaterais são semelhantes. Cada triângulo equilátero é invariante por três simetrias axiais(2) e duas rotações cujo centro O é tanto o centro de gravidade, o ortocentro quanto o centro dos círculos inscritos e circunscritos ao triângulo. Esta é uma figura notável.
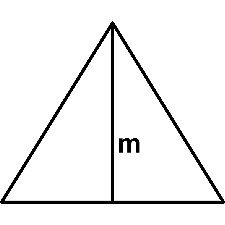 Construção da primeira bissetriz, mediador, mediador e eixo de simetria axial.
Construção da primeira bissetriz, mediador, mediador e eixo de simetria axial.
De cima baixamos um m direito na metade oposta. Este direito tem a propriedade da bissecção (compartilha o ângulo de 60 graus em dois ângulos de 30 graus); tem a propriedade da mediana desde que começa do topo para o meio do lado oposto; ele também tem a propriedade do mediador, uma vez que é perpendicular para o lado e é levantado no meio deste lado. Finalmente, o m direito é o eixo da simetria axial, uma vez que divide o triângulo equilátero em dois retângulos notáveis.
Três eixos perfeitos de simetria
Podemos começar dos picos A e B da direita nos lados opostos, tendo as mesmas propriedades descritas anteriormente com o m direito.
Temos 3 eixos de simetria perfeitos, AD; BE e CF.
Centro de rotação do triângulo
Ponto O é um centro rotacional
Podemos virar o triângulo em si mesmo.
Primeira tradução axial: O ponto B assume o lugar do ponto A, o ponto A assume o lugar do ponto C, e o ponto C assume o lugar do ponto B. Você tem uma figura idêntica, ou inalterada, com uma rotação superior.
Segunda tradução axial: O ponto C assume o lugar da Ponte B, o Ponto B assume o lugar do ponto A, e o ponto A assume o lugar do ponto C. Você tem uma figura idêntica ou inalterada, com uma rotação superior.
Há apenas duas rotações axiais porque se continuarmos encontramos a figura inicial com a base AB e o topo C
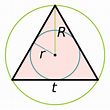 O triângulo equilateral está inscrito em um círculo, mas um círculo também está inscrito neste triângulo.
O triângulo equilateral está inscrito em um círculo, mas um círculo também está inscrito neste triângulo.
Por outro lado, sempre sobre este centro de gravidade O, este centro O também é o centro do círculo passando por suas três cúpulas abc. O triângulo equilateral está, portanto, inscrito em um círculo. Assim, carrega o infinito rotativo do círculo por seus três picos. Mas também pode conter um círculo que é tangente ao triângulo equilátero no meio dos três lados EFD e assim, desta vez, o círculo está inscrito no triângulo equilátero. Simbolicamente, o triângulo equilátero, portanto, também contém o infinito rotativo do círculo. Simbolicamente realmente notável…
 O triângulo equilátero pode conter um número infinito de triângulos equiláteros.
O triângulo equilátero pode conter um número infinito de triângulos equiláteros.
Tudo que você tem que fazer é encaixá-los em cada triângulo e superar o meio de cada lado. Cada vez, você tem um triângulo equilátero com metade do comprimento do anterior. Mais uma vez, é simbolicamente interessante. Como um lembrete, a matemática e, claro, a geometria que faz parte dela, intervém em objetos matemáticos que são símbolos lógicos, resultantes da abstração e muitas vezes do valor numérico intrínseco. Objetos matemáticos sempre envolvem lógica estrita, ou seja, apenas abstração lógica. Entendemos o sucesso desse tipo de símbolos na maçonaria, sabendo que o símbolo está estruturando nos indivíduos.
Assimimetrias e rotações são automorfismos
Mas onde se torna literalmente vertiginoso é que as transformações, que mantêm a figura inalterada (simetria axial e rotação central) são chamadas em automorfismos matemáticos. Não sei se isso é devido ao acaso, mas a correlação com a frase-chave do regime escocês retificado provoca uma profunda reflexão. De acordo com o regime escocês retificado, o homem é de fato um deus automorfismo! Como um lembrete, “o homem é a imagem imortal de Deus, mas que será capaz de reconhecê-la se ele mesmo desfigurá-la.”
(1) ternário como modus operandi (processo operacional)
(2) uma simetria é propriedade de um sistema ou de uma figura: é quando duas partes são semelhantes. O exemplo mais conhecido é a simetria da geometria. De um modo geral, um sistema é simétrico quando você pode trocar seus elementos deixando sua forma inalterada. O conceito de auto-mudança ajuda a esclarecer essa definição.
(3) Um automorfismo é um isomorfismo (transformação que retém as características inalteradas) de um objeto matemático X em si mesmo. Na maioria das vezes, é uma bijeção de X em X que preserva a “estrutura” de X. Pode ser visto como uma simetria X. Os automorfismos de X formam um grupo. A definição abstrata do automorfismo é a seguinte: é um endomorfismo que é ao mesmo tempo um isomorfismo. Em outras palavras, é um morfismo de um objeto X de uma determinada categoria em si, que também é um isomorfismo. Simplificando, existem transformações que mantêm as características das figuras inalteradas
